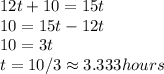Question

Ben and Sam set out together on bicycle traveling at 15 and 12 miles per hour, respectively. After 40 minutes, Ben stops to fix a flat tire. If it takes Ben one hours to fix that flat tire and Sam continues to ride during this time, how many hours will it take Ben to catch up to Sam assuming he resumes his ride at 15 miles per hour?

Answer 1

3.333 hours

Explanation:

First, you need the distance that Ben (
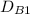`D_(B1)`) and Sam (
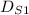`D_(S1)`) have traveled in 40 minutes (Multiply the time by the speed):

`t=40 min( (1 hour)/(60 min))=2/3 hours\\D_(B1)=2/3(15)=10 miles\\D_(S1)=2/3(12)=8 miles`

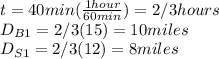
While Ben is fixing the flat tire Sam keeps going, the distance traveled by Sam (
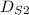`D_(S2)` in one hour is:

`D_(S2)=1(12)=12 miles`

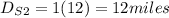
At this moment the distance traveled by Ben is in total 10 miles, the total distance traveled by Sam is 20 miles, and the distance between them is 10 miles. Let
`x` be the distance from the position when Ben fixed its tire to the position when he catches up with Sam, and
`t` the time

`x=15t`

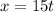
The distance traveled by Sam at the same time t is
`x-10`.

`x-10=12t\\x=12t+10`

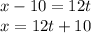
Substitute this equation in the other and solve for
`t`:

`12t+10=15t\\10=15t-12t\\10=3t\\t=10/3\approx3.333hours`