a. Any vector in the span of
 is a linear combination of the vectors in
is a linear combination of the vectors in
 . The simplest one we could come up with is the addition of the two vectors we know:
. The simplest one we could come up with is the addition of the two vectors we know:
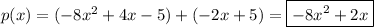
b. Since one vector is quadratic while the other is purely linear, there is no choice of
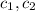 such that
such that
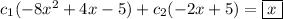
because the only way to eliminate the
 term is to pick
term is to pick
 , but there's no way to eliminate the remaining constant term.
, but there's no way to eliminate the remaining constant term.