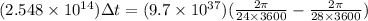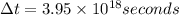Question

Zorch, an archenemy of Superman, decides to slow Earth’s rotation to once per 28.0 h by exerting an opposing force at and parallel to the equator. Superman is not immediately concerned, because he knows Zorch can only exert a force of 4.00×107N (a little greater than a Saturn V rocket’s thrust). How long must Zorch push with this force to accomplish his goal?

Answer 1

`\Delta t = 3.95 * 10^(18) seconds`

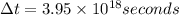
Step-by-step explanation:

Torque due to applied force along its surface is given as

`\tau = r * F`

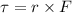
here we know that

r = radius of earth =
`6.37 * 10^6 m`

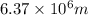
Now we have

`\tau = (6.37 * 10^6)(4.00 * 10^7)`

`\tau = 2.548 * 10^(14) Nm`

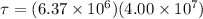
now we know that

initial angular speed of Earth is

`\omega_i = (2\pi)/(24* 3600)`

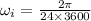
final angular speed will be

`\omega_f = (2\pi)/(28* 3600)`

so now we have

`\tau \Delta t = I(\omega_i - \omega_f)`

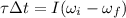
here we have moment of inertia of Earth is given as

`I = (2)/(5) mR^2`

`I = (2)/(5)(5.98 * 10^(24))(6.37 * 10^6)^2`

`I = 9.7 * 10^(37) kg m^2`

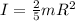
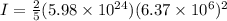
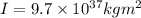
now we have

`(2.548 * 10^(14))\Delta t = (9.7 * 10^(37))((2\pi)/(24* 3600) - (2\pi)/(28* 3600))`

`\Delta t = 3.95 * 10^(18) seconds`