Question

The fire department needs information on friction losses occurring between a water main and an open fire hydrant. At maximum main pressure (85 psig), the water discharge rate is 1620 gpm through a 2.5-inch open fire hydrant. The water main, in which the velocity is very small, is situated 8 ft below the hydrant discharge point. Determine the friction loss from the main to the discharge point. Assume atmospheric pressure is 15 psia.

Answer 1

Step-by-step explanation:

The given data is as follows.

`P_(1)` = 85 psig,
`P_(2)` =
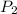`P_(atm)` = 15 psia

Q = 1620 gpm, d = 2.5 inch, l = 8 ft = 2.4384 m

According to Darey-Weisbach equation,

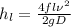`h_(l) = (4fl \\u^(2))/(2gD)` ......... (1)

Value of 'f' will be decided on the basis of Reynold number.

As, it is known that
`R_(l) = (\rho \\u d)/(\mu)`

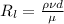
where,
`\mu_(water)` =
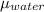`10^(-3)` kg/ms

As it is known that 1 gpm =
`(1)/(3.67) m^(3)/hr`

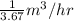
So,
`1 m^(3)/hr` = 3.67 gpm

Therefore, Q =
`1620 * (1)/(3.67)`

=
`441.4168 m^(3)/hr`

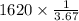
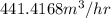
= 0.1226
`m^(3)/s`

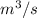
In, 1 inch = 2.54 cm = 0.0254 m

Therefore, d = 2.5 \times 0.0254 = 0.0635 m

V =
`(Q)/((\pi)/(4)d^(2))`

=
`(0.1226)/(0.785 * (0.0635)^(2))`

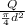
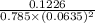
= 38.73 m/s

Hence, we will calculate Reynold number as follows.

`R_(l)` =
`(1000 * 38.73 * 0.0635)/(10^(-3))`

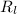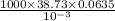
= 2459355

As
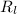`R_(l)` > 2000 then, it means that flow is turbulent.

As, f = 0.079
`R^(-0.25)_(l)`

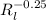
= 0.001994

Putting all the values into equation (1) formula as follows.

`h_(l) = (4fl \\u^(2))/(2gD)`

=
`(4 * 0.001994 * 2.4384 * (38.73)^(2))/(2 * 9.81 * 0.0635)`

=
`1.04069 * 10^(5) m`

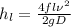
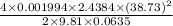
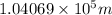
Thus, we can conclude that friction loss from the main to the discharge point is
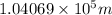`1.04069 * 10^(5) m`.