Question

A laser beam passes through a diffraction grating and the second order bright spot is porodced at an angle of 22 degress from the main central axis. What is the highest order spot that can be produced by this arrangment?

Answer 1

The highest order spot is 5.33.

Step-by-step explanation:

Given that,

Angle = 22°

Order number = 2

In a laser diffraction experiment, the condition for constructive interference or bright spot is

`d\sin\theta=m\lambda`

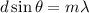
Put the value into the formula

`d\sin22=2\lambda`

`(d)/(\lambda)=(\sin22)/(2)`

`(d)/(\lambda)=0.1873`

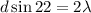
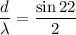
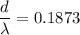
The maximum grating for

`\theta=90^(\circ)`

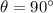
We need to calculate the highest order spot

Using formula of the highest order spot

`m=(d\sin\theta)/(\lambda)`

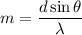
Put the angle into the formula

`m=(d)/(\lambda)`

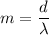
Put the value into the formula

`m=(1)/(0.1873)`

`m=5.33`

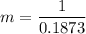
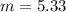
Hence,The highest order spot is 5.33.