I'm not sure what to make of "yp" and "ye ns", or the given initial conditions, so I'll let you handle that and just focus on the general solution.

The corresponding homogeneous ODE has characteristic equation
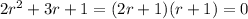
with roots at
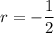 and
and
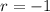 , so the characteristic solution to the ODE is
, so the characteristic solution to the ODE is
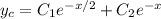
For the non-homogeneous ODE, assume a solution of the form
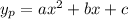
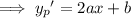
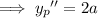
Substituting
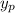 and its derivatives into the ODE gives
and its derivatives into the ODE gives
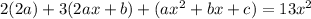

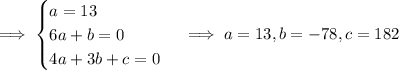
so that the particular solution is

and the general solution is
