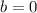Question

suppose you want to solve the equation 2a + b = 2a, where a and b are nonzero real numbers. Describe the solution to this equation. Justify your description.

Answer 1

Answer and explanation:

In this problem, we have the following equation:

`2a+b=2a`

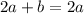
And the problem states that
`a` and
`b` are nonzero real numbers. First of all, we need to assume that
`a` and
`b` are nonzero real numbers. Thus, let's say that:

`a=1 \\ \\ b=1`

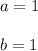
Plug in the equation, we have:

`2(1)+(1)=2(1) \\ \\ 2+1=2 \\ \\ 3=2 \ Absurd!`

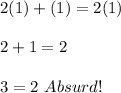
As you can see, we got an absurd statement since
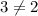`3\\eq 2`. Then, the only possible solution is that
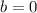`b=0`. So, we can write our equation as follows:

`2a+b=2a \\ \\ 2a+(0)=2a \\ \\ 2a=2a \ True!`

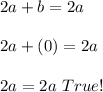
Conclusion:

For any real number
`a`, we will have that
`b=0`