Question

A series RLC circuit has a resistance of 74.31 Ω, a capacitance of 4.11 μF, and an inductance of 292.39 mH. The circuit is connected to a variable-frequency source with a fixed rms output of 81.68 V . If the source frequency is 60 Hz, calculate Z .

Answer 1

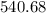`540.68` ohm

Step-by-step explanation:

R = resistance of the resistor = 74.31 ohm

f = source frequency = 60 Hz

C = Capacitance of the capacitor = 4.11 x 10⁻⁶ F

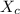`X_(c)` = capacitive reactance of capacitor

capacitive reactance of capacitor is given as

`X_(c) = (1)/(2\pi fC)`

`X_(c) = (1)/(2(3.14)(60)(4.11* 10^(-6)))`

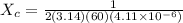
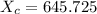`X_(c) = 645.725` ohm

L = Inductance of inductor = 293.39 mH = 0.29239 H

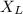`X_(L)` = Inductive reactance of Inductor

Inductive reactance of Inductor is given as

`X_(L) = 2\pi fL`

`X_(L) = 2(3.14) (60) (0.29239)`

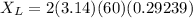
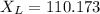`X_(L) = 110.173` ohm

Impedance is given as

`Z = \sqrt{R^(2) + (X_(L) - X_(c))^(2)}`

`Z = \sqrt{74.31^(2) + (110.173 - 645.725)^(2)}`

`Z = \sqrt{74.31^(2) + (110.173 - 645.725)^(2)}`

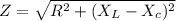
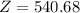`Z = 540.68` ohm