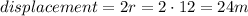Question

Help me please to do those problems...

1. Michelle walks 100m toward the west, then turns and walks back the way she came 20m.
What is her distance? What is her displacement?
race.

2. An Olympic runner competing in the 1600m circles the track exactly 4 times during
What is his distance? What is his displacement?

3. A shopper walks forward 20m, turns right and walks 5m, turns left and walks in the original
direction 10m, then turns left again for 5m. What is her distance? What is her
displacement?

4. Some hikers travel 2 km north, turn toward the west and travel 4km, turn toward the
south and travel 6 km, then finally travel east for 4 km. What is their distance? What is
their displacement?

5. A skating rink is perfectly circular and it has a radius of 12m. A skater circles the rink on the
outer edges near the wall. When the skater is half way around the circle what is her
distance and what is her displacement?​

Answer 1

Keeping in mind that:

- Distance is the length of the total path covered by the person, regardless of the directions of the different parts of motion

- Displacement is just the distance in a straight line between the final point and the initial point

Let's apply these concepts to solve the different parts of the problem:

1. 120 m, 80 m west

The total distance is the sum of the length of the different paths:

distance = 100 + 20 = 120 m

To find the displacement, we need to find the distance between the starting point and the ending point. Assuming the starting point as

x = 0

Michelle moved 100 m westward and 20 m eastward, so the ending point is at

ending point = 100 - 20 = 80 m (westward)

So, the displacement is

displacement = 80 - 0 = 80 m (west)

2. 6400 m, 0

The distance is equal to the length of the track multiplied by the number of laps, so:

`distance = 1600 \cdot 4 = 6400 m`

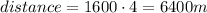
The track is circular, and the runner completes exactly 4 laps: it means that at the end of the motion, the runner is at her starting point. So ending point and starting point coincide, and so the displacement

displacement = ending point - starting point = 0

3. 40 m; 10 m forward

The total distance is just the sum of the lengths of the different parts of the motion, so:

distance = 20 + 5 + 10 + 5 = 40 m

The find the displacement, we need to assign signs to every direction:

Forward --> positive along the forward-backward direction

Backard --> negative along the forward-backward direction

Right --> positive direction along the right-left direction

Left --> negative direction along the right-left direction

Along the forward-backward direction, the displacement is:

20 m forward and 10 m backward, so 20 - 10 = 10 (forward)

Along the left right direction, the displacement is:

5 m right and 5 m left, so 5 - 5 = 0

So the net displacement is 10 m (forward)

4. 16 km; 4 km south

Again, t total distance is the sum of the lengths of the different parts of the motion, so:

distance = 2 + 4 + 6 + 4 = 16 km

To find the displacement, we assign signs to every direction:

North --> positive along the north-south direction

south --> negative along the north-south direction

east --> positive direction along the east-west direction

west --> negative direction along the east-west direction

Along the north-south direction, the displacement is:

2 km north and 6 km south, so 2 - 6 = -4 km (4 km south)

Along the east-west direction, the displacement is:

4 km east and 4 km west, so 4 - 4 = 0

So the net displacement is 4 km south

5. 37.7 m; 24 m

The distance covered by the skater is the length of half circumference, so given the radius

r = 12 m

The distance is

`distance= \pi r = \pi \cdot (12)=37.7 m`

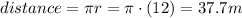
The displacement is the distance in a straight line between the ending position and the starting position. Since the skater ends her motion halfway around the circle, the distance between the initial and final point is equal to the diameter of the circle (two times the radius). So,

`displacement = 2r = 2 \cdot 12 = 24 m`