Question

Define an equivalence relation P on Z as follows: Let x,y e Z ; xPy if and only if ke Z s.t. x - y = 2k Show how the reflexive property and symmetric property of equivalence relations hold for P on Z.

Answer 1

Answer with Step-by-step explanation:

We are given that an equivalence relation P on Z as

Let
`x,y\in Z`

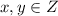
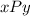`xPy` if and only if
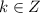`k\in Z` such that x-y=2k.

We have to show that how the reflexive property and symmetric property of an equivalence relations hold for P on Z.

We know that reflexive property

a is related to a by given relations.

If xPax then we get

`x-x=0=2(0)`

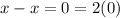
Where k=0 and 0 belongs to integers.

Hence, the relation satisfied reflexive property.

Symmetric property :If a is related to b then b is related to b.

If x and y is related by the relation

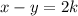`x-y=2k` where k is any integer

`y-x=-2k=2(-k)`

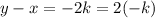
k belongs to integers.

Hence, relation satisfied symmetric property.