Question

What is the energy of each of the two photons produced in an electron-positron annihilation?

Use the following Joules-to-electron-Volts conversion 1eV = 1.602 × 10-19 J.
The rest mass of an electron is 9.11×10^-31 kg

Answer 1

511797.76 eV

Step-by-step explanation:

Mass of electron = Mass of positron = 9.11×10⁻³¹ kg

Mass of annihilation

Δm = Mass of electron + Mass of positron

⇒Δm = 9.11×10⁻³¹+9.11×10⁻³¹

From Einstein's Equation

`E=\Delta c^2\\\Rightarrow E=18.22* 10^(-31)* (3* 10^8)^2\ J`

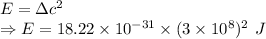
1 eV = 1.602 × 10⁻¹⁹ J

`(18.22* 10^(-31)* (3* 10^8)^2)/(1.602* 10^(-19))=1023595.51\ eV`

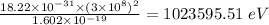
Energy of each photon is

`(1023595.51)/(2)=511797.76\ eV`

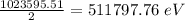
∴ Energy of each of the two photons produced in an electron-positron annihilation is 511797.76 eV