1 Answer

Amr Osama · Answer 1 · 2020-05-09T03:20:33+0000

Since 1986 = 62*32 + 2, we have

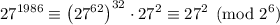
$27^(1986)\equiv\left(27^(62)\right)^(32)\cdot27^2\equiv27^2\pmod{2^6}$

by Euler's theorem, since
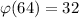$\varphi(64)=32$ . Then

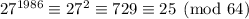
$27^(1986)\equiv27^2\equiv729\equiv25\pmod{64}$

which tells us the 7th digit from the right is 1.

Then

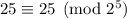
$25\equiv25\pmod{2^5}$

so the next digit must be 0;

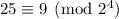
$25\equiv9\pmod{2^4}$

so the next digit is 1;

$9\equiv1\pmod{2^3}$

so the next digit is 1;

$1\equiv1\pmod{2^2}$

so the next digit is 0;

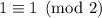
$1\equiv1\pmod2$

so the next digit is 0; and

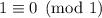
$1\equiv0\pmod1$

so the last digit is 1.

So the last 7 digits of this number in binary are 1011001.

Please log in or register to add a comment.