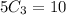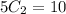Question

(4) Let S = {a,b,c,d,e}. (a) List all of the 2-permutations of S in an organized manner. How many are there?

(b) List all of the 2-combinations of S in an organized manner. How many are there?
(c) List all of the 3-combinations of S in an organized manner. How many are there?
(d) On the previous page, you should have gotten the same number of 2-combinations of S as 3-combinations. Explain why we should expect these numbers to be the same.

Answer 1

Answer with Step-by-step explanation:

We are given that a set S={a,b,c,d,e}

a.We have n=5

We have to find the number of 2-permutations of S in an organised manner

Using permutation formula

`nP_r=(n!)/(r!(n-r)!)`

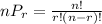
r=2

`5P_2=(5!)/(3!)`

`5P_2=(5* 4*3!)/(3!)`

`5P_2=20`

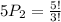
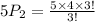
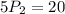
Hence, the total number 2- permutations of S =20

{a,b},{b,c},{c,d},{d,e},{a,c},{a,d},{a,e},{b,d},{b,e},{c,e},{b,a},{c,b},{d,c},{e,d},{c,a},{d,a},{e,a},{d,b},{e,b},{e,c}.

b.We have to find the 2- combinations of S in an organised manner

By using combination formula

`nC_r=(n!)/(r!(n-r)!)`

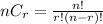
n=5,r=2

`5C_2=(5!)/(2!(5-2)!)`

`5C_2=(5* 4*3!)/(2!3!)`

`5C_2=10`

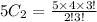
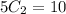
Hence, the number of 2 -combinations of S =10

{a,b},{b,c},{c,d},{d,e},{a,c},{a,d},{a,e},{b,d},{b,e},{c,e}.

c.We have n=5 r=3

Using combination formula

`5C_3=(5!)/(3!(5-3)!)`

`5C_3=(5* 4* 3!)/(3!2!)`

`5C_3=10`

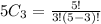
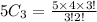
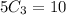
Hence, the total number of 3- combinations of S =10

{a,b,c},{b,c,d},{c,d,e},{a,b,d},{a,b,e},{b,c,e},{a,c,d},{a,d,e},{b,d,e},{a,c,e}.

d.Number of 2 -combinations of S=Number of 3- combinations of S=10

Combinations is a selection of r elements out of n elements.

When we select 3 elements out of 5 then we get total number of combinations of S=10 and when we select 2 elements out of 5 then we get total number of combinations of S=10

By combinations formula

`5C_3=10`

`5C_2=10`