Answer: The correct answer is Option D.
Step-by-step explanation:
We are given a nucleus having representation:
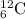
Number of protons = 6
Number of neutrons = 12 - 6 = 6
Number of electrons = 6
To calculate the mass defect of the nucleus, we use the equation:
![\Delta m=[(n_p* m_p)+(n_n* m_n)+(n_e* m_e)]-M](https://img.qammunity.org/2020/formulas/physics/college/1wwg0qa0nzxsnh4g8iicp4gyd8vncno25n.png)
where,
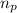 = number of protons = 6
= number of protons = 6
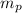 = mass of one proton = 1.00728 u
= mass of one proton = 1.00728 u
 = number of neutrons = 6
= number of neutrons = 6
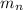 = mass of one neutron = 1.00866 u
= mass of one neutron = 1.00866 u
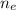 = number of electrons = 6
= number of electrons = 6
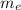 = mass of one electron = 0.00054858 u
= mass of one electron = 0.00054858 u
M = Mass number = 12
Putting values in above equation, we get:
![\Delta m=[(6* 1.00728)+(6* 1.00866)+(6* 0.00054858)]-12\\\\\Delta m=0.098931u](https://img.qammunity.org/2020/formulas/physics/college/zngqrjdrfubj99vga41ut8w7pcuziwotx4.png)
To calculate the binding energy of the nucleus, we use the equation:
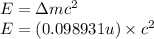
 (Conversion factor:
(Conversion factor:
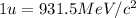 )
)
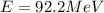
Hence, the correct answer is Option D.