Question

Find the generating function for the sequence 1,-2,4,-8, 16, ...

Answer 1

Answer:-3+double the number

Step-by-step explanation: It started off as -3 so to get the next answer you double the number and change the sign for each number.

Answer 2

`a(x)=(1)/(1+2x)`

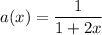
Explanation:

The generating function a(x) produces a power series ...

`a(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots`

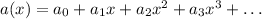
where the coefficients are the elements of the given sequence.

We observe that the given sequence has the recurrence relation ...

`a_0=1;a_n=-2a_(n-1) \quad\text{for n $>$ 0}`

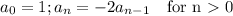
This can be rearranged to ...

`a_n+2a_(n-1)=0`

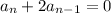
We can formulate this in terms of a(x) as follows, then solve for a(x).

`\sum\limits^(\infty)_(n=1) {a_(n)x^n} =a(x)-a_0 \quad\text{and}\\\\\sum\limits^(\infty)_(n=1) {2a_(n-1)x^n} =(2x)a(x) \quad\text{so}\\\\\sum\limits^(\infty)_(n=1) {(a_n+2a_(n-1))x^n}=0=a(x)-a_0+2xa(x)\\\\a(x)=(a_0)/(1+2x)=(1)/(1+2x)`

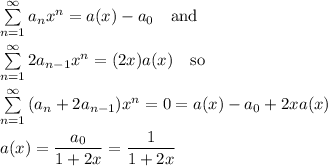
The generating function is ...

a(x) = 1/(1+2x)