Question

True or false: To find the number of outcomes of disjoint sets, add the number of outcomes for each event.

Answer 1

The statement is True.

Explanation:

Disjoint sets do not share any common element, which means for given 2 disjoint sets A and B we can write.

`n(A\cap B)=0`

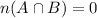
Then we can verify the statement using the definition of inclusion-exclusion principle.

Verifying the statement.

According to the inclusion-exclusion principle the number of elements in any two finite sets is given by

`n(A\cup B) = n(A)+n(B)-n(A \cap B)`

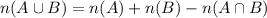
But we know for disjoint sets we have

`n(A\cap B)=0`

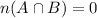
Thus replacing on the formula for the principle we get

`n(A\cup B) = n(A)+n(B)-0`

`n(A\cup B) = n(A)+n(B)`

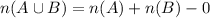
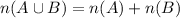
Thus we have verified that the number of outcomes of disjoint sets is equal to the number of outcomes of each event, which is the number of elements of each set. Therefore we have a true statement