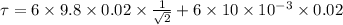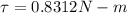Question

A 6kg robot is required to climb a 45 degree incline. The wheel radius is 20mm, what torque is required to drive the robot at a constant rate? The robot must accelerate at up to 10 mm/s^2. What torque is required?

Answer 1

Given:

mass of robot, m = 6 kg

radius of the wheel, r = 20 mm = 0.02 m

acceleration, a = 10
`mm/s^(2) = 10* 10^(-3) m/s^(2)`

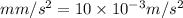
acceleration due to gravity, g = 9.8
`m/s^(2)`

inclination,
`\theta = 45^(\circ)`

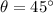
Solution:

Refer to fig 1

Force is given by:

F = mgsin
`\theta`

Torque is given by:

Torque,
`\tau = F* r = mgrsin\theta`

`\tau = 6* 9.8* 0.02* sin45`

`\tau = 6* 9.8* 0.02* \frac{1}{\sqrt {2}}`

`\tau = 0.83 N-m`

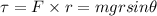
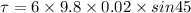
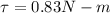
Refer to fig 2.

Provided the acceleration of the wheel, the Force and torque is now:

Force, F = mgsin
`\theta + ma`

Torque,
`\tau = F* r = Mgrsin\theta + Mar`

`\tau = 6* 9.8* 0.02* \frac{1}{\sqrt {2}} + 6* 10* 10^(-3)* 0.02`

`\tau = 0.8312 N-m`