Answer:
The coefficient of static friction is 0.578.
Step-by-step explanation:
Given that,
Mass of coin = 54 gm
Revolution r = 1.0
Distance = 14.4 cm
We need to calculate the force when the coin located more than 14.4 cm from the axis of rotation
Using formula of centripetal force
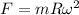
Where, m = mass
R = radius
Put the value into the formula
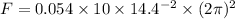
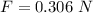
We need to calculate the coefficient of static friction
Using formula of friction
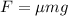
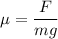
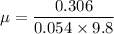
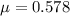
Hence, The coefficient of static friction is 0.578.