Answer:
12 Model P televisions
28 Model Q televisons.
Explanation:
Let
 be the number of Model P sold and
be the number of Model P sold and
 the number of Model Q sold. This problem has 4 unknown variables. With the information on the problem you can write some equations:
the number of Model Q sold. This problem has 4 unknown variables. With the information on the problem you can write some equations:
The total of television sold was 40:
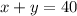
The average of the selling price was $141:
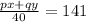
The Model P sold for $30 less than the other model:
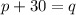
With only three equation, is needed to test them with q=120 and p=120
if
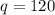

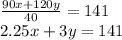
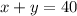
Solving the system of equation by the method of elimination (Multiply this equation
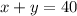 by -3):
by -3):
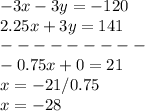
Substitute the value of
 in one of the equations:
in one of the equations:
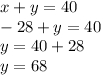
With a
 greater than 40 and a negative value of
greater than 40 and a negative value of
 , this can't be the solution.
, this can't be the solution.
if
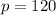
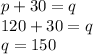

Solving the system of equation by the method of elimination (Multiply this equation
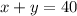 by -3):
by -3):
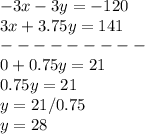
Substitute the value of
 in one of the equations:
in one of the equations:
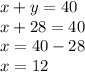
They sold 12 Model P televisions and 28 Model Q televisions.