Question

A series circuit is composed of three resistors:

R1= 7
R2 = 6
R3 = 11

A 12-volt battery is connected across the three resistors.
Find the total resistance Rt.

A. 2.5
B. 0.40
C. 24

____ omega

Answer 1

Resistors in a series = R1 + R2 + R3

Rt = 7 + 6 + 11

= 24 omega

Answer 2

Equivalent resistance of the combination is 24 ohms.

Step-by-step explanation:

Resistance 1,
`R_1=7\ \Omega`

Resistance 2,
`R_2=6\ \Omega`

Resistance 3,
`R_3=11\ \Omega`

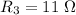
Voltage of battery, V = 12 volt

These three resistors are connected in series whose equivalent is given by :

`R_(eq)=R_1+R_2+R_3`

`R_(eq)=7+6+11`

`R_(eq)=24\ \Omega`

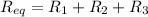
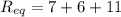
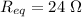
So, the equivalent resistance of the combination is 24 ohms. Hence, this is the required solution.