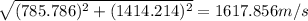Answer:
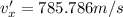
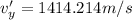 (decreasing)
(decreasing)
Given:
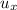 = 2300 m/s
= 2300 m/s
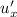 = 100 m/s
= 100 m/s
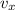 = 2000 m/s
= 2000 m/s
Angle made with the horizontal,
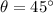
The horizontal component of velocity is on the X-axis whereas the vertical one is on the Y-axis
Now, by the law of conservation of momentum for horizontal axis:
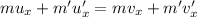
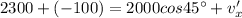
(The mass of the particles is same)
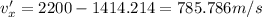
Now, by the law of conservation of momentum for vertical axis:
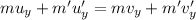
(The mass of the particles is same)
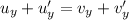
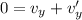
(since, initially, there's no vertical component of velocity)
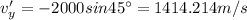 (decreasing)
(decreasing)
velocity, v =
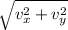
v =