L :V --> W is a linear transformation. Prove each of the following (a) ker L is a subspace of V. (b) range L is a subspace of W. - QAmmunity.org

L :V --> W is a linear transformation. Prove each of the following (a) ker L is a subspace of V. (b) range L is a subspace of W.

asked Dec 28, 2020 1.2k views

1 Answer

Answer:

a) Assume that
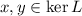$x,y\in\ker L$ , and
$\alpha$ is a scalar (a real or complex number).

First. Let us prove that
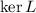$\ker L$ is not empty. This is easy because
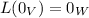L(0_V)=0_W , by linearity. Here,
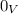0_V stands for the zero vector of V, and
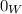0_W stands for the zero vector of W.

Second. Let us prove that
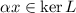$\alpha x\in\ker L$ . By linearity

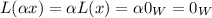$L(\alpha x) = \alpha L(x)=\alpha 0_W=0_W$ .

Then,
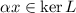$\alpha x\in\ker L$ .

Third. Let us prove that
$y+ x\in\ker L$ . Again, by linearity

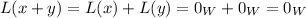L(x+y)=L(x)+L(y) = 0_W + 0_W=0_W .

And the statement readily follows.

b) Assume that
and
are in range of
. Then, there exist
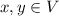$x,y\in V$ such that
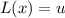L(x)=u and
L(y)=v .

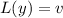First. Let us prove that range of
is not empty. This is easy because
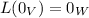L(0_V)=0_W , by linearity.

Second. Let us prove that
$\alpha u$ is on the range of
.

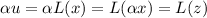$\alpha u = \alpha L(x) = L(\alpha x) = L(z)$ .

Then, there exist an element
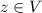$z\in V$ such that
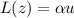$L(z)=\alpha u$ . Thus
$\alpha u$ is in the range of
.

Third. Let us prove that
u+v is in the range of
.

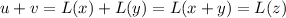u+v = L(x)+L(y) = L(x+y)=L(z) .

Then, there exist an element
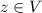$z\in V$ such that
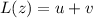L(z)= u +v . Thus
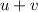u +v is in the range of
.

Notice that in this second part of the problem we used the linearity in the reverse order, compared with the first part of the exercise.

Explanation:

Paras answered Jan 3, 2021

by Paras

5.3k points

Search QAmmunity.org