Answer:
The displacement of the air drop after 3 second is 18.27 m.
Step-by-step explanation:
Mass of the rain drop = m =
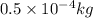
Weight of the rain drop = W
Duration of time = t = 3 seconds
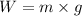
Drag force on rain drop =

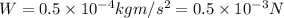
Motion of the rain drop:
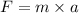
Net force on the rain drop , F= W - D

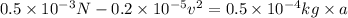
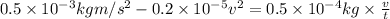
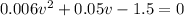
v = 12.18 m/s
Initial velocity of the rain drop = u = 0 (since, it is starting from rest)
v=u+at (First equation of motion)
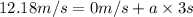
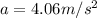
 (second equation of motion)
(second equation of motion)
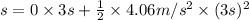
s = 18.27 m
The displacement of the air drop after 3 second is 18.27 m.