A particle moves with acceleration function a(t) = 5 + 4t - 2t^2. Its initial velocity v(0) = 3 m/s and its initial displacement is s(0) = 10 m. Find its position after 4 second…

Question

asked Jun 5, 2020 129k views

1 Answer

Samuel Gfeller · Answer 1 · 2020-06-11T09:59:25+0000

Answer:

Its position after 4 seconds is 62 meters.

Step-by-step explanation:

It is given that,

The acceleration of the particle is given by equation :

a(t)=5+4t-2t^2

Also,
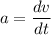
a=(dv)/(dt)

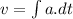
$v=\int\limits {a.dt}$

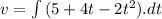
$v=\int\limits {(5+4t-2t^2).dt}$

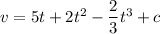
v=5t+2t^2-(2)/(3)t^3+c

At t = 0,
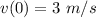$v(0)=3\ m/s$ . So, c = 3

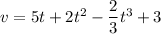
v=5t+2t^2-(2)/(3)t^3+3

Also,
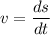v=(ds)/(dt) , s is the position

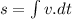
$s=\int\limits {v.dt}$

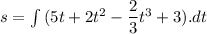
$s=\int\limits {(5t+2t^2-(2)/(3)t^3+3).dt}$

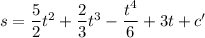
s=(5)/(2)t^2+(2)/(3)t^3-(t^4)/(6)+3t+c'

At t = 0,
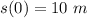$s(0)=10\ m$ . So, c' = 10

s=(5)/(2)t^2+(2)/(3)t^3-(t^4)/(6)+3t+10

At t = 4 s

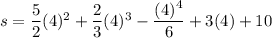
s=(5)/(2)(4)^2+(2)/(3)(4)^3-((4)^4)/(6)+3(4)+10

s = 62 m

So, at t = 4 seconds the position of the particle is 62 meters. Hence, this is the required solution.