Question

The life span of a certain insect​ (in days) is uniformly distributed over the interval left bracket 15.29 right bracket . A. What is the expected life of this​ insect? B. Find the probability that one of these​ insects, randomly​ selected, lives longer than 24 days.

Answer 1

The exercise says that the life variable is measured in days, that is, it is a discrete distribution, this because it takes finite and punctual values, 21, 22, 23 days, etc., not 21 and a half days or 23 and a quarter days.

Now, the discrete uniform distribution assumes that the probability of each value it takes is equal.

In this case the distribution takes 15 values, from 15 to 29 including the extremes, so the probability of each value is
`(1)/(n)` =
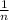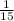`(1)/(15)`, so the probability mass function will be:

`f(x)=\left \{ {{(1)/(15),x=15,16,..,28,29} \atop {0, else}} \right.`

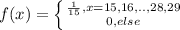
With this we can calculate the probability that an insect, selected at random, lives more than 24 days, like this:

`P (x> 24) = f (25) + f (26) + f (27) + f (28) + f (29) + f (30) + f (31) ...\\P (x> 24) = (1)/(15) + (1)/(15) + (1)/(15) + (1)/(15) + (1)/(15) + 0 + 0 + ...\\P (x> 24) = (5)/(15) = (1)/(3)`

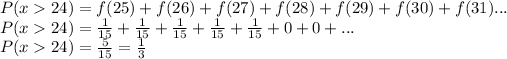
On the other hand, the expected life or average life in this distribution is calculated as follows:
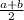`(a+b)/(2)` that this case is
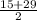`(15+29)/(2)` = 22

Answer

A) The awakened life of the insect is 22 days

B) The probability that an insect, selected at random, lives more than 24 days is 1/3 = 0.33 = 33.3%