Answer:
The zeros of the polynomial function are 1, -3, 3+i and 3-i.
Explanation:
The given function is
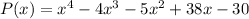
We can find a zero of the given function by hit and trial method.
Substitute x=1 in the given function.
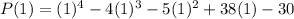
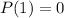
The value of function is 0 at x=1 it means (x-1) is a factor of given function.
Substitute x=-3 in the given function.
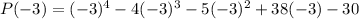
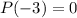
The value of function is 0 at x=-3 it means (x+3) is a factor of given function.
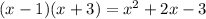
Divide the given function by
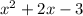 , to get remaining factors.
, to get remaining factors.
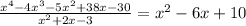
So, the factor form of given function is
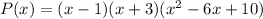
Quadratic formula: If a quadratic equation is
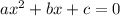 , then
, then
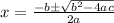
Using quadratic formula find the zeroes of
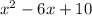 .
.
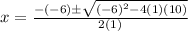
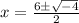
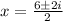
![[\because √(-1)=i]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7t7d5c5krhm8hxlkwuabv87yojfn9bl2p8.png)
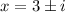
Therefore the zeros of the polynomial function are 1, -3, 3+i and 3-i.