Question

Find the Critical points of dy/dx=15-2y-y^2 and determine if they are stable, unstable or semi-stable.

Answer 1

3...stable critical value, -5 unstable critical vale

Explanation:

A critical value of the given differential is a value
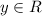`y \in \mathh{R}` such that the left hand side of the equation is equal to zero, i.e, y such that

`0=15 - 2y -y^2=-(-15+2y+y^2)=-(x+5)(x-3)`

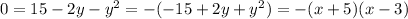
By the last equation the critical values of the given differential equation are y=-5, 3.

Now, since

`(dy)/(dx)=-(y+5)(y-3)`

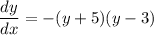
It holdst that

`(dy)/(dx) < 0 \quad \text{for} \quad x>3`

and

`(dx)/(dy)>0 \quad \text{for} \quad -5<x<3`

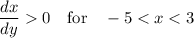
hence 3 is a stable critical value.

Also note that

`(dx)/(dy)>0 \quad \text{for} \quad -5 < x <3`

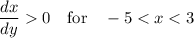
and

`(dx)/(dy) < 0 \quad \text{for } \quad x<-5`

hence -5 is an unstable critical value.