Question

[5 pts] Describe how and why the formula for permutations differs from the formula for combinations 4.

Answer 1

Permutations formula
`P(n,k)=(n!)/((n-k)!)`.

Combinations formula
`C(n,k)=(n!)/(k!(n-k)!)`

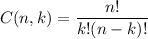
Explanation:

The premutations formula gives us the number of ways that we can choose k elements of a set of n elements, taking into account the order in which we choose the elements and is given by

`P(n,k)=(n!)/((n-k)!)`

The formula for combinations gives us the numbers of ways that we can choose k elements of a set of n elements without taking into account the order of the object. It's is given by

`C(n,k)=(n!)/(k!(n-k)!)`

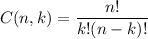
Ex: Let us take the set of letters
`\mathbf{L}=\{A \quad B \quad C \quad D\}`

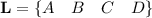
- C(4,2) gives us the number of pairs of letters that we can form with the letters from the set
`\mathbf{L}`, in this case we the pairs AB and BA are the same.

-P(4,2) gives us the number of pairs of letters that we can form with the letters from the ser
`\mathbf{L}` taking into acount the order of the pair, in this case the pairs AB and BA are different.