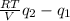Question

Consider a tank having one inlet molar flowrate qi and one outlet molar flowrate q. It is assumed that the pressure of the gas in the tank is P, the volume of the tank is V and temperature is T. The ideal gas law can be applied. If the volume V and temperature T are constant, find how the pressure varies with time.

Answer 1

Step-by-step explanation:

Let inlet flow rate =
`q_(1)`

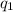
and, outlet flow rate =
`q_(2)`

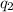
Also, it is known that
`q_(2) - q_(1)` =
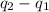`(dn)/(dt)` ....... (1)

where, n = number of moles accumulating in tank

According to ideal gas equation, PV = nRT

Hence, P =
`(nRT)/(V)`

`(dP)/(dt)` =
`((RT)/(V)) (dn)/(dt)`

`(dn)/(dt)` =
`((V)/(RT)) (dp)/(dt)`

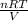
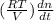
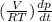
As it is given that T and V are constant. Hence, from equation (1) and (2) we get the following.

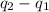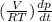
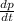`q_(2) - q_(1)` =
`((V)/(RT)) (dp)/(dt)`

`(dp)/(dt)` =
`(RT)/(V) q_(2) - q_(1)`