Question

A car accelerates from rest with an acceleration of 5 m/s^2. The acceleration decreases linearly with time to zero in 15 s, after which the car continues with constant speed. At what time t will the car have moved 500 m from its starting point?

Answer 1

Answer: At time 18.33 seconds it will have moved 500 meters.

Step-by-step explanation:

Since the acceleration of the car is a linear function of time it can be written as a function of time as

`a(t)=5(1-(t)/(15))`

`a=(d^(2)x)/(dt^(2))\\\\\therefore (d^(2)x)/(dt^(2))=5(1-(t)/(15))`

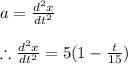
Integrating both sides we get

`\int (d^(2)x)/(dt^(2))dt=\int 5(1-(t)/(15))dt\\\\(dx)/(dt)=v=5t-(5t^(2))/(30)+c`

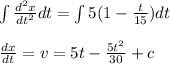
Now since car starts from rest thus at time t = 0 ; v=0 thus c=0

again integrating with respect to time we get

`\int (dx)/(dt)dt=\int (5t-(5t^(2))/(30))dt\\\\x(t)=(5t^(2))/(2)-(5t^(3))/(90)+D`

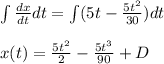
Now let us assume that car starts from origin thus D=0

thus in the first 15 seconds it covers a distance of

`x(15)=2.5* 15^(2)-\farc{15^(3)}{18}=375m`

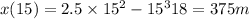
Thus the remaining 125 meters will be covered with a constant speed of

`v(15)=5* 15-(15^(2))/(6)=37.5m/s`

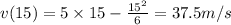
in time equalling
`t_(2)=(125)/(37.5)=3.33seconds`

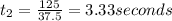
Thus the total time it requires equals 15+3.33 seconds

t=18.33 seconds