Answer:

Explanation:
We can write this rate as an ordinary differential equation.
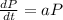
Where a is proportional constant, P the population variable, and t the time.
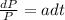
Integrating each side of the equation.

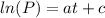
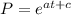
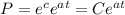
To find C we need to use the initial condiction, it means evaluae P at t=0.

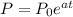
Now, we use the sentence the population has doubled in 5 years.
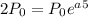
We can find "a" in this condition.

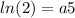
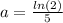
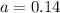
Finally, let's find how long will it take to triple.
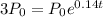
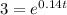
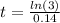

I hope it helps you!