Question

A pion lives 26 ns in its rest frame. It travels 15 cm down a beam pipe in a particle accelerator before it decays into other particles. How far is this in the rest frame of the pion?

Answer 1

Step-by-step explanation:

It is given that,

Life time of a pion,
`t=26\ ns=26* 10^(-9)\ s`

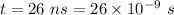
Distance covered by a pion, d = 15 cm = 0.15 m

We need to find distance from the rest frame of the pion. Firstly, we can calculate the speed of the pion as :

`v=(d)/(t)`

`v=(0.15)/(26* 10^(-9))`

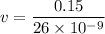
v = 5769230.76 m/s

or

`v=5.76* 10^6\ m/s`

Its length in the rest frame is given by the formula as :

`d_o=d\sqrt{1-(v^2)/(c^2)}`

`d_o=0.15\sqrt{1-((5.76* 10^6)^2)/((3* 10^8)^2)}`

`d_o=0.149\ m`

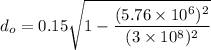
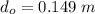
or

`d_o=14.9\ cm`

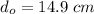
So, the length of the pion in rest frame is 14.9 cm. Hence, this is the required solution.