Question

Numeric passwords of length r consist of n digits from {0,1,2,…,9}. Digits may be not repeated (e.g., 1178 is a not a permissible password of length 4). Find the smallest value of r such that the number of possible passwords of length r is greater than 2,000,000.

Answer 1

The smallest value of r such that there are more than 2,000,000 possible passwords is r=9.

Explanation:

Given : Numeric passwords of length r consist of n digits from {0,1,2,…,9}. Digits may be not repeated (e.g., 1178 is a not a permissible password of length 4).

To Find : The smallest value of r such that the number of possible passwords of length r is greater than 2,000,000.

Solution :

Numeric passwords of length r consist of n digits from {0,1,2,…,9}

i.e. There are 10 possible digits : 0,1,2,3,4,5,6,7,8,9.

So, The first digit have 10 ways,

Second digit have 9 ways different from previous digit.

Third digit have 8 ways different from previous digit.

Similarly, r th digit have n-r+1 ways.

Applying fundamental counting principle,

If the first event occur in m ways and second event occur in n ways the the number of ways two events occur in sequence is
`m\cdot n`

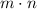
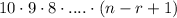`10\cdot 9\cdot 8\cdot ....\cdot (n-r+1)` is the required ways.

But The smallest value of r such that the number of possible passwords of length r is greater than 2,000,000.

i.e.
`10\cdot 9\cdot 8\cdot ....\cdot (n-r+1)\geq 2000000`

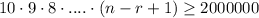
The increasing value of r will obtain more than 2,000,000 possible passwords were,

If r=1

Number of passwords = 10

If r=2

Number of passwords =
`10\cdot 9=90`

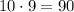
If r=3

Number of passwords =
`10\cdot 9\cdot8=720`

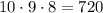
If r=4

Number of passwords =
`10\cdot 9\cdot8\cdot 7=5040`

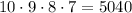
If r=5

Number of passwords =
`10\cdot 9\cdot8\cdot 7\cdot 6=30240`

If r=6

Number of passwords =
`10\cdot 9\cdot8\cdot 7\cdot 6\cdot 5=151200`

If r=7

Number of passwords =
`10\cdot 9\cdot8\cdot 7\cdot 6\cdot 5\cdot 4=604800`

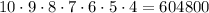
If r=8

Number of passwords =
`10\cdot 9\cdot8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3=1814400`

If r=9

Number of passwords =
`10\cdot 9\cdot8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2=3628800`

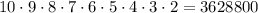
For r = 9 the password length exceeds.

Therefore, The smallest value of r such that there are more than 2,000,000 possible passwords is r=9.