Question

Use mathematical induction to prove the following statement: 8"-1 is a multiple of 7 for all neN

Answer 1

Answer: with Step-by-step explanation:

We are given that

P(n)=
`8^n-1`

We have to prove that given statement is a multiple of 7 using mathematical induction for all natural numbers n belongs to N.

Suppose n=1

Then P(1)=8-1=7

Hence, it is a multiple of 7 .Therefore, it is true for n=1

We suppose that it is true for n=k

Then P(k)=
`8^k-1` is a multiple of 7.

We shall prove that it is true for n=k+1

P(k+1)=
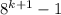`8^(k+1)-1` is a multiple of 7

LHS=
`8^(k+1)-1`

=
`8^k\cdot8-1`

=
`8^k\cdot8-8+8-1`

=
`8(8^k-1)+7`

=
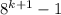
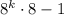
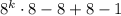
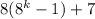
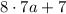`8\cdot 7a+7` because
`8^k-1` is a multiple of 7 therefore
`8^k-1=7a`

=
`7(8a+1)`

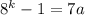
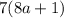
P(k+1) is a multiple of 7.

Therefore, P(n) is true for all natural numbers belongs to N.

Answer 2

Explanation:

To prove that
`8^n-1` is a multiple of 7.

Proof by induction:

Let n =1. Then we have 8-1 =7 is a multiple of 7

Thus the P(1) is true.

Let us assume that P(n) is true.

`8^n-1` = 7l is true for some integer l

To check for P(n+1)

`8^(n+1) -1`=LHS

=
`8^n(8)-1\\=(7l+1)8-1\\=56l+7\\=7(8l+1)`

Thus we find that this is also a multiple of 7.

If true for n, then true for n+1

Hence we find that since true for 1, we have it is true for all natural numbers.