Question

Dez pours water (n 1.333) into a container made of crown glass (n 1.52). The light ray in ner made of crown glass (n = 1.52). The light ray in glass incident on the glass-to-liquid boundary makes an angle of 30.0 with the normal. Find the angle of the corresponding refracted ray

Answer 1

The angle of the corresponding refracted ray is 34.84°

Step-by-step explanation:

Given that,

Refractive index of water n= 1.33

Refractive index of glass n= 1.52

Incident angle = 30.0°

We need to calculate the refracted angle

Using formula of Snell's law

`n_(i)\sin i=n_(r)\sin r`

Put the value into the formula

`\sin r=(n_(i)\sin i)/(n_(r))`

`\sin r=(1.52*\sin30)/(1.33)`

`\sin r=0.5714`

`r=sin^(-1)0.5714`

`r = 34.84^(\circ)`

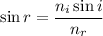
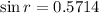
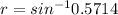
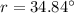
Hence, The angle of the corresponding refracted ray is 34.84°