Question

Consider the real vector space V = R 4 . For each of the following five statements, provide either a proof or a counterexample. (a) dim V = 4. (b) span((1, 1, 0, 0),(0, 1, 1, 0),(0, 0, 1, 1)) = V . (c) The list ((1, −1, 0, 0),(0, 1, −1, 0),(0, 0, 1, −1),(−1, 0, 0, 1)) is linearly independent. (d) Every list of four vectors v1, . . . , v4 ∈ V , such that span(v1, . . . , v4) = V , is linearly independent. (页码61).

Answer 1

Answer with Step-by-step explanation:

We are given that a real vector space

V=
`R^4`

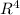
a.We have to prove that dim V =4

Let (a,b,c,d) is an element of V

Suppose that four elements

(1,0,0,0),(0,1,0,0),(0,0,1,0) and (0,0,0,1)

a(1,0,0,0)+b(0,1,0,0)+c(0,0,1,0)+d(0,0,0,1)

=(a,b,c,d)

All four elements are independent and can span each element of V.

Hence, dimension of V=4

b.We are given that (1,1,0,0),(0,1,1,0,(0,0,1,1)

We have to prove that these elements can span V

If number of elements are less than dimension of then the elements can not span V.

`\left[\begin{array}{cccc}1&1&0&0\\0&1&1&0\\0&0&1&1\end{array}\right]`

Rank of matrix =3

Hence, rank is less than the dimension of V.Therefore, given elements can not span V.

c.We are given that (1,-1,0,0),(0,1,-1,0),(0,0,1,-1),(-1,0,0,1)

We have to show that these elements are linearly independent.

`\left[\begin{array}{cccc}1&-1&0&0\\0&1&-1&0\\0&0&1&-1\\-1&0&0&1\end{array}\right]`

Every row or column is not a linear combination of other rows or columns.

Therefore, these elements are linearly independent.

d.We are given that
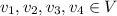`v_1,v_2,v_3,v_4\in V` and span
`(v_1,v_2,v_3,v_4)=V`

We have to prove that given vectors are linear independent.

Let
`v_1=(1,0,0,0),v_2=(0,1,0,0),v_3=(0,0,1,0),v_4=(0,0,0,1)`

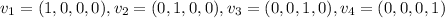
(a,b,c,d)=a(1,0,0,0)+b(0,1,0,0)+c(0,0,1,0)+d(0,0,0,1)

All four vectors are linearly independent because any element is not a linear combination other elements .

Hence, every four vectors
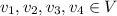`v_1,v_2,v_3,v_4\in V` are linearly independent.