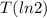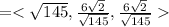Question

Find the unit tangent vector at the given value of t for the following parameterized curves.

r(t)= ⟨7–√e^t,3e^t,3e^t⟩

, for 0≤t≤1
; t=ln 2

Answer 1

`T(ln2)`
`= <√(145) , (6√(2) )/(√(145) ) , (6√(2) )/(√(145) ) >`

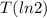
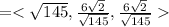
Explanation:

Given :
`r(t)=<7-√(e^t), 3e^t,3e^t > .........(i)`

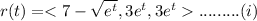
We first have to differentiate of equation
`(i)`

`r'(t) = < (√(e^t) )/(2) , 3e^t,3e^t> ..........(ii)`

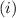
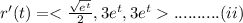
Now to get a unit tangent vector at the given value of
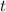`t`, we put
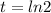`t = ln2` in equation
`(ii)`

`r'(ln2) = < \frac{\sqrt{e^(ln2)} }{2} , 3e^(ln2),3e^(ln2)>`

`= <(1)/(√(2) ) ,6,6>` [∵
`e^(lna)=a`]

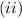
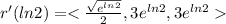
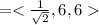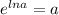Now to get a unit tangent vector , we will divide our vector
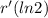`r'(ln2)` by its magnitude. So let's first find the magnitude.

`|r'(ln2)|=\sqrt{((1)/(√(2) ) )^2 +6^2+6^2}`

`= \sqrt{(1)/(2)+36+36 }`

`= \sqrt{(145)/(2) }`

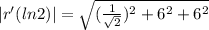
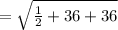
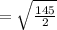
Now we can find the our unit tangents vector.

`T(ln2)=(r'(ln2))/(|r'(ln2)|)`

`= \frac{<(1)/(√(2)) ,6,6> }{\sqrt{(145)/(2)} }`

`= <\frac{(1)/(√(2) ) }{\sqrt{(145)/(2)} } ,\frac{6}{{\sqrt{(145)/(2)} }}, \frac{6}{{\sqrt{(145)/(2)} }} >`

`= <√(145) , (6√(2) )/(√(145) ) , (6√(2) )/(√(145) ) >`

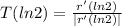
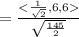
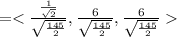
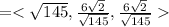
Hence,
`T(ln2)`
`= <√(145) , (6√(2) )/(√(145) ) , (6√(2) )/(√(145) ) >`