Answer:
a) 24
b) 3.3 sec
c) 29.8 m/s
d) 48.85 m
Step-by-step explanation:
a)
α = angular acceleration = - 28.4 rad/s²
r = radius of the tire = 0.32 m
w₀ = initial angular velocity = 93 rad/s
w = final angular velocity = 0 rad/s
θ = angular displacement
Using the equation
w² = w₀² + 2αθ
0² = 93² + 2 (- 28.4) θ
θ = 152.3 rad
n = number of revolutions
Number of revolutions are given as
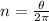
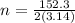
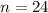
b)
t = time taken to stop
using the equation
w = w₀ + αt
0 = 93 + (- 28.4) t
t = 3.3 sec
c)
v₀ = initial velocity of the car
initial velocity of the car is given as
v₀ = r w₀ = (0.32) (93) = 29.8 m/s
d)
v = final velocity = 0 m/s
a = linear acceleration = rα = (0.32) (- 28.4) = - 9.09 m/s²
d = distance traveled by car before stopping
Using the equation
v² = v₀² + 2 a d
0² = 29.8² + 2 (- 9.09) d
d = 48.85 m