Question

You are on a 4 m high ladder and throw a ball upwards at 12 m/s. It lands on the ground below the ladder.

a) How long was the ball in the air?
b) What was the final velocity?

Answer 1

a) 2.75 s

The vertical position of the ball at time t is given by the equation

`y= h+ut-(1)/(2)gt^2`

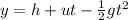
where

h = 4 m is the initial height of the ball

u = 12 m/s is the initial velocity of the ball (upward)

g = 9.8 m/s^2 is the acceleration of gravity (downward)

We can find the time t at which the ball reaches the ground by substituting y=0 into the equation:

`0 = 4 + 12t - 4.9 t^2`

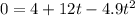
This is a second-order equation. By solving it for t, we find:

t = -0.30 s

t = 2.75 s

The first solution is negative, so we discard it; the second solution, t = 2.75 s, is the one we are looking for.

b) -15.0 m/s (downward)

The final velocity of the ball can be calculated by using the equation:

`v=u-gt`

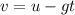
where

u = 12 m/s is the initial (upward) velocity

g = 9.8 m/s^2 is the acceleration of gravity (downward)

t is the time

By subsisuting t = 2.75 s, we find the velocity of the ball as it reaches the ground:

`v=12 -(9.8)(2.75)=-15.0 m/s`

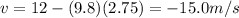
And the negative sign means the direction is downward.