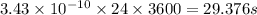Question

A satellite orbits the Earth in the same direction it rotates in a circular orbit above the equator a distance of 250 km from the surface. By how many seconds per day will a clock on such a satellite run slow compared to a clock on the Earth? (Compute just the special relativistic effects.)

Answer 1

Clock on the satellite is slower than the one present on the earth = 29.376 s

Given:

Distance of satellite from the surface, d = 250 km

Step-by-step explanation:

Here, the satellite orbits the earth in circular motion, thus the necessary centripetal force is provided by the gravitation force and is given by:

`(mv^(2))/(R) = (GMm)/(R^(2))`

where

v = velocity of the satellite

R = radius of the earth = 6350 km = 6350000 m

G = gravitational constant =
`6.674* 10^(- 11) m^(3)/ks-s^(2)`

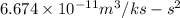
M = mass of earth =
`5.972* 10^(24) kg`

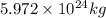
Therefore, the above eqn can be written as:

`v = \sqrt{(GM)/(R)}`

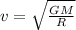
Now, for relativistic effects:

`(v)/(c) = \sqrt{(GM)/(Rc^(2))} = 26.41* 10^(- 6)`

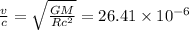
Now,

r = R + 250

`(v_(surface))/(c) = {(1)/(c)(2\pi R)/(24) = 1.54* 10^(-6)`

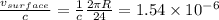
Ratio of rate of satellite clock to surface clock:

`\frac{\sqrt{1 - (v^(2))/(c^(2))}}{\sqrt{1 - (v_(surface)^(2))/(c^(2))}} = 3.43* 10^(-10)`

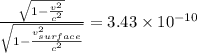
Clock on the satellite is slower than the one present on the earth:

`3.43* 10^(-10)* 24* 3600 = 29.376 s`