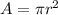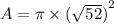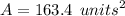Question

Given a diameter with endpoints P(-12,-8) and Q(0,0),find the center coordinate circumstance and area of the circle described

Answer 1

Center:(-6,-4)

Circumference:45.31

Area:163.4

Explanation:

The given circle has diameter with endpoints P(-12,-8) and Q(0,0).

The center is the midpoint of P(-12,-8) and Q(0,0).

We use the midpoint rule to find the center.

`( (x_2+x_1)/(2), (y_2+y_1)/(2) )`

`( ( - 12 + 0)/(2) , ( - 8 + 0)/(2) ) = ( - 6, - 4)`

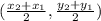
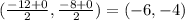
Use the distance formula to find radius using the center (-6,-4) and the point on the circle (0,0) or (-12,-8).

`d = √((x_2-x_1)^2 +(y_2-y_1)^2)`

`r = \sqrt{( { - 6 - 0)}^(2) + ( { - 4 - 0)}^(2) }`

`r = √(36 + 16) = √(52)`

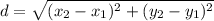
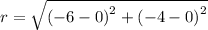
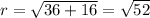
The circumference is

`C=2\pi \: r`

`C=2 \: \pi \: * √(52)`

`C=45.31 \: units`

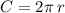
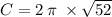
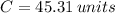
The area is given by:

`A=\pi {r}^(2)`

`A=\pi * {( √(52) )}^(2)`

`A=163.4 \: \: {units}^(2)`