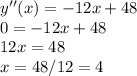Question

Find all relative extrema and inflection points for the following function. 4) y -2x^3+24x^2+288 x-35

Answer 1

Relative maximum at x=12

Relative minimum at x=-4

Inflection point at x=4

Explanation:

To find all the critical points of the function we need the first derivative of the function

`y(x)=-2x^3+24x^2+288x-35\\y'(x)=-2(3)x^(3-1)+24(2)x^(2-1)+288(1)\\y'(x)=-6x^2+48x+288`

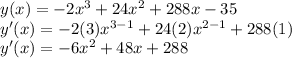
According to Fermat's theorem, it will be a critical point in y'(x)=0, then

`y'(x)=-6x^2+48x+288\\0=-6x^2+48x+288\\\\-6x^2+48x+288=0\\-6(x^2-8x-48=0\\x^2-8x-48=0\\(x-12)(x+4)=0\\x_1=12\\x_2=-4\\`

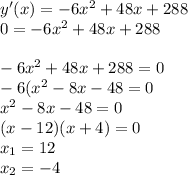
With the test of the second derivative, we can know if the points are relative extrema or inflections.

`y'(x)=-6x^2+48x+288\\y''(x)=-6(2)x^(2-1)+48(1)\\y''(x)=-12x+48`
`y''(12)=-12(12)+48\\y''(12)=-144+48=-96`

`y''(-4)=-12(-4)+48\\y''(-4)=48+48=96`

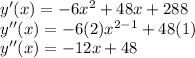
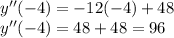
The second derivative test says: if
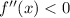`f''(x)<0` then x is a relative maximum, if
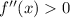`f''(x)>0` then x is a relative minimum. So x=12 is a relative maximum and x=-4 is a relative minimum.

To find the inflection point y''(x)=0

`y''(x)=-12x+48\\0=-12x+48\\12x=48\\x=48/12=4`