Step-by-step explanation:
Given that,
Resistance R = 75.0 ohms
Inductance L = 55.0 mH
Capacitance
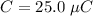
Voltage V = 12.0 V
Frequency f = 60.0 Hz
We need to calculate the angular frequency
Using formula of angular frequency
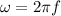
Put the value into the formula
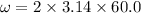
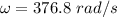
(a). We need to calculate the value of
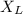
Using formula of
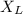
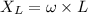
Put the value into the formula
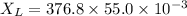
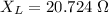
(b). We need to calculate the value of
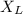
Using formula of
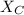
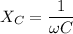
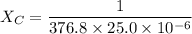
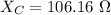
(c). We need to calculate the value of Z
Using formula of impedance
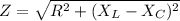
Put the value into the formula
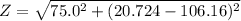
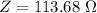
(d). We need to calculate the rms current
Firstly we need to calculate the current
Using formula of current
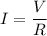
Put the value into the formula
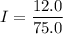
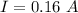
Using formula of rms current
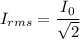
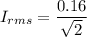
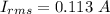
(e). We need to calculate the rms voltage across the resistor
Using formula of rms voltage
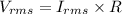
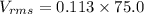
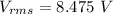
(f). We need to calculate the rms voltage across the inductor
Using formula of rms voltage
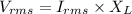
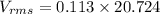
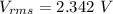
(g). We need to calculate the rms voltage across the capacitor
Using formula of rms voltage
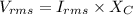
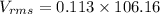
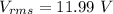
(h). We need to calculate the dissipated power by the circuit
Using formula of dissipated power
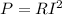
Put the value into the formula
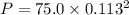
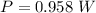
Hence, This is the required solution.