Question

A wheel with a weight of 396 N comes off a moving truck and rolls without slipping along a highway. At the bottom of a hill it is rotating at an angular velocity of 22.7 rad/s. The radius of the wheel is 0.569 m and its moment of inertia about its rotation axis is 0.800 MR^2 . Friction does work on the wheel as it rolls up the hill to a stop, at a height of above the bottom of the hill; this work has a magnitude of 3476 J . Calculate "h" Use 9.81 for the acceleration due to gravity.

Answer 1

The height is 5.67 m.

Step-by-step explanation:

Given that,

Weight = 396 N

Angular velocity = 22.7 rad/s

Radius = 0.569 m

Moment of inertia = 0.800 kg-m²

Work = 3476 J

We need to calculate the kinetic energy

Using formula of kinetic energy

`K.E =(1)/(2)mv^2+(1)/(2)I\omega^2`

Put the value into the formula

`K.E=(1)/(2)*(369)/(9.81)*0.569*(22.7)^2+(1)/(2)*0.800*(22.7)^2`

`K.E=5720.43\ J`

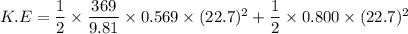
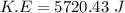
We need to calculate the renaming energy

`E=5720.43-3476=2244.43\ J`

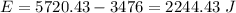
We need to calculate the height

Using formula of potential energy

`mgh =2244.43`

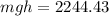
Put the value into the formula

`h=(2244.43)/((396)/(9.81)*9.81)`

`h=5.67\ m`

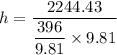
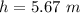
Hence, The height is 5.67 m.