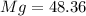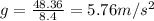Answer:
Part a)
M = 8.4 kg
Part b)

Step-by-step explanation:
As we know that wire is of mass 4.30 g and length 47.9 cm
so here we can find the mass per unit length of the wire as

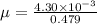
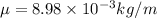
now for fundamental mode of the frequency we know that
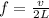
so we have
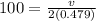
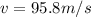
now we have
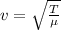
so we have
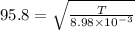
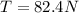
so the weight will be
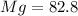

Part b)
Now on another planet we have
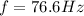
so we have

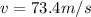
now we have
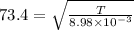
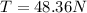
so the weight will be