Answer: a) v2f = 0.83 m/s b) The distance will be 0.3738 m.
Explanation: a) When two bodies collide with each other with definite velocity, the system is a closed system, which means, there are no other forces acting on it, and the linear momentum is constant. So, for a system of two bodies:
Qi = Qf
m1v1i + m2v2i = m1v1f + m2v2f
2.3 + 4.(-2) = 2.(-3.66) + 4v2f
v2f =
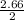
v2f = 0.83
The final velocity of mass m2 is v2f = 0.83 m/s.
b) Since m1 slides with coefficient of friction, there is a force of friction acting on it:
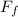 = μ·
= μ·
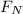 , where
, where
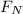 is a normal force acting on m1.
is a normal force acting on m1.
As there is no up or down movement,
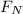 =
=
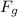 = m.g = 2*9.8
= m.g = 2*9.8
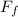 = 0.6*2*9.8
= 0.6*2*9.8
Only the force of friction is acting on m1, so:
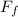 = m.a
= m.a
0.6*2*9.8 = 2*a
a = 5.88 m/s²
Using
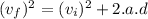
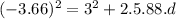
d =
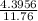
d = 0.3738
The mass m1 traveled 0.3738 m before it came to rest.