Question

An object is located 13.5 cm in front of a convex mirror, the image being 7.05 cm behind the mirror. A second object, twice as tall as the first one, is placed in front of the mirror, but at a different location. The image of this second object has the same height as the other image. How far in front of the mirror is the second object located?

Answer 1

Second object is located at 42.03 cm in front of mirror

Step-by-step explanation:

In this question we have given,

object distance from convex mirror ,u=-13.5cm

Image distance from convex mirror,v=7.05cm

let focal length of convex mirror be f

we have to find the distance of second object from convex mirror

we know that u, v and f are related by following formula

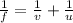`(1)/(f) =(1)/(v)+ (1)/(u)`.............(1)

put values of u and v in equation (1)

we got,

`(1)/(f) =(1)/(7.05)+ (1)/(-13.5)`

`(1)/(f)=(13.5-7.05)/(13.5* 7.05)`

`(1)/(f)=(6.45)/(13.5* 7.05)\\f=13.5* 1.09\\f=14.75`

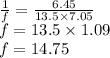
we have given that

second object is twice as tall as the first object

and image height of both objects are same

it means

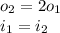`o_(2)=2o_(1)\\i_(1)=i_(2)`.............(2)

we know that

`(v)/(u)=(i)/(o)\\i=(o* v)/(u)`

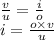
therefore,

`i_(1)=(o_(1)* v)/(u)`.................(3)

put values of v and u in equation 3

`i_(1)=-(o_(1)* 7.05)/(13.5)`

`i_(1)=-0.52o_(1)`

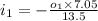
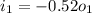
therefore from equation 2

`i_(2)=-0.52o_(1)`

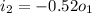
we know that

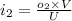`i_(2)=(o_(2)* V)/(U)`.................(4)

put value of
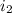`i_(2)` and
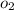`o_(2)` in equation 4

`-.52o_(1)=(2o_(1)* V)/(U)`

`U=(2o_(1)* V)/(-.52o_(1)) \\U=-3.85V`

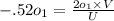
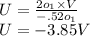
we know that U,V and f are related by following formula

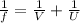`(1)/(f) =(1)/(V)+ (1)/(U)`.............(5)

put values of f and U in equation 5

we got

`(1)/(14.75) =(1)/(V)- (1)/(3.85V)`

`(1)/(14.75) =(2.85)/(3.85V)`

`(1)/(14.75) =(2.85)/(3.85V)\\V=(2.85* 14.75)/(3.85)\\V=10.91 cm`

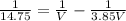
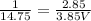
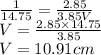
Therefore,

U=-10.91\times 3.85

U=-42.03 cm

Second object is located at 42.03 cm in front of mirror