Question

In an oscillating LC circuit with L equals 0.048 H and C = 4uF the current is initially a maximum. How long in ms will it take before the capacitor is fully charged for the first time?

Answer 1

The times is 0.688 ms.

Step-by-step explanation:

Given that,

Inductance L= 0.048 H

Capacitor C= 4\mu F

The current is initially maximum

`I=I_(max)`

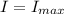
We know that,

`I=I_(max)\cos\omega t`

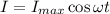
Where,
`\omega=(1)/(√(LC))`

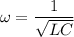
We need to calculate the time

`(dq)/(dt)=I`

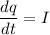
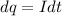`dq=Idt`....(I)

On integrating equation (I)

`\int_(0)^(q){dq}=\int_(0)^(t){I_(max)\cos\omega t}dt`

`q=I_(max)((\sin\omega t)/(\Omega))_(0)^(t)`

`q=(I_(max))/(\omega)\sin\omega t`

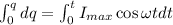
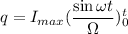
If
`q = q_(max)`

`\sin\omega t=1`

`\omega t=(\pi)/(2)`

`t =(\pi)/(2\omega)`

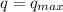
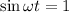
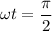
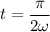
Put the value of
`\omega`

`t=(\pi)/(2*(1)/(√(LC)))`

`t=(\pi√(LC))/(2)`

`t=(\pi)/(2)√(LC)`

`t=(\pi)/(2)\sqrt{0.048*4*10^(-6)}`

`t=0.688\ msec`

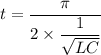
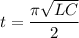
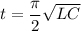
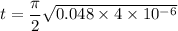
Hence, The times is 0.688 ms.