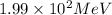Question

An isotope of californium-252 undergoes a spontaneous fission, producing cesium-135, 3 neutrons, and one other isotope. a) Determine the identity of the other isotope produced in the fission, and write out the reaction equation, using full isotopic notation, for example Pm → C022 + Seag + 2n. b) Calculate the amount of mass (in u) lost during this fission. The masses of the three isotopes are: 252.081 626 u (californium), 134.905 978 u (cesium), 113.935 880 u (unknown). Maintain a precision of no less than 7 SF as you work. c) Calculate the energy (in MeV) released by this fission, accurate to 3 SF.

Answer 1

For a: The isotopic symbol of unknown element is
`_(43)^(114)\textrm{Tc}`

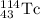
For b: The amount of mass lost during this process is 0.2137730 u.

For c: The energy released in the given nuclear reaction is
`1.99* 10^2MeV`

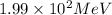
Step-by-step explanation:

• For a:

In a nuclear reaction, the total mass and total atomic number remains the same.

For the given fission reaction:

`^(252)_(98)\textrm{Cf}\rightarrow ^A_Z\textrm{X}+^(135)_(55)\textrm{Cs}+3^1_0\textrm{n}`

• To calculate A:

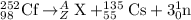
Total mass on reactant side = total mass on product side

252 = A + 135 + 3

A = 114

• To calculate Z:

Total atomic number on reactant side = total atomic number on product side

98 = Z + 55 + 0

Z = 43

Hence, the isotopic symbol of unknown element is
`_(43)^(114)\textrm{Tc}`

• For b:

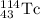
We are given:

Mass of
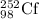`_(98)^(252)\textrm{Cf}` = 252.081626 u

Mass of
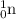`_(0)^(1)\textrm{n}` = 1.008665 u

Mass of
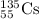`_(55)^(135)\textrm{Cs}` = 134.905978 u

Mass of
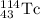`_(43)^(114)\textrm{Tc}` = 113.935880 u

To calculate the mass defect, we use the equation:

`\Delta m=\text{Mass of reactants}-\text{Mass of products}`

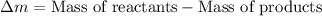
Putting values in above equation, we get:

`\Delta m=(m_(Cf))-(m_(Cs)+m_(Tc)+3m_(n))\\\\\Delta m=(252.081626)-(134.905978+113.935880+3(1.008665))=0.2137730u`

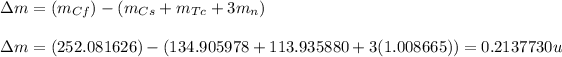
Hence, the amount of mass lost during this process is 0.2137730 u.

• For c:

To calculate the energy released, we use the equation:

`E=\Delta mc^2\\E=(0.2137730u)* c^2`

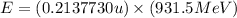`E=(0.2137730u)* (931.5MeV)` (Conversion factor:
`1u=931.5MeV/c^2` )

`E=1.99* 10^2MeV`

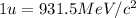Hence, the energy released in the given nuclear reaction is
`1.99* 10^2MeV`