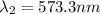Question

In a double-slit experiment, light from two monochromatic light sources passes through the same double slit. The light from the first light source has a wavelength of 645 nm. Two different interference patterns are observed. If the 8th order bright fringe from the first light source coincides with the 9th order bright fringe from the second light source, what is the wavelength of the light coming from the second monochromatic light source?

Answer 1

`\lambda_2 = 573.3 nm`

Step-by-step explanation:

As we know that the position of maximum intensity on the screen is given as

`y = (N\lambda L)/(d)`

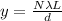
here we know that

`\lambda` = wavelength

L = distance of the screen

d = distance between two slits

now we know that the position of 8th maximum intensity is same as that of 9th maximum on the screen

so we have

`(N_1\lambda_1 L)/(d) = (N_2 \lambda_2 L)/(d)`

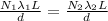
so here we have

`8 (645 nm) = 9 \lambda_2`

`\lambda_2 = 573.3 nm`